パルストランス(GDT)の設計
こんにちはkentamuです。前回の記事で触れたパルストランス(GDT、ゲートドライブトランス)の設計方法を紹介します。
そもそもトランスって?
トランスとはトランスフォーマー(変圧器)のことで、高磁性体(磁化されやすい)コアにコイルがまかれたような構造をしています。
プラスチックのボビンにコイルがまかれる様子

フェライトのコアをボビンの上下からサンドイッチして完成したトランス

トランスの解体図。左から、フェライトコア、ボビン、フェライトコア。

回路図は以下の通りです。
T1の文字の下にある2本線がコアを示し、コイルに打ってある・(ドット)が巻き始めを意味します。下の回路図ですと、同じコアに3つのコイルが巻かれていることになります。

信号が入力されるコイルを1次コイル、信号が伝達される側のコイルを2次コイルといいます。回路図ですと、1-2が1次、3-4,5-6が2次コイルです。
では、どやって信号を伝達しているのでしょうか?
答えは簡単です。コアの持つ磁気エネルギーを利用しています。
まず、1次コイルに入った電気エネルギーにより、コアに磁気エネルギーが発生します。そして、同じコアにまかれた2次コイルに磁気エネルギーの影響で電気エネルギーが発生します。
電気エネルギー → 磁気エネルギー → 電気エネルギー
このような順番でエネルギーが伝達されます。
つまり、トランスは電気的に絶縁しながら信号を伝達してくれるパーツとなります。
トランスの動作とB-H曲線
電子工作をしていると、時々目にするのがヒステリシス曲線(B-H曲線)です。
本項ではヒステリシス曲線について、トランスの動作を交えながら考えていきます。

トランスの動作
1.電流と磁界
コイルがまかれているとき、コイルに電流が流れると磁界が発生します。これが磁気エネルギーの発端です。磁界はHで表します
2.磁界と磁束密度
コアにコイルがまかれていて磁界が発生すると、コアの透磁率(磁界の通しやすさ)に比例して、磁束密度というものが決定します。透磁率はμ、磁束密度はBで表します。コアは空気よりも透磁率がとても大きいですから、空芯コイルよりも大きな磁束密度を持たせることができます。
3.磁束密度と磁束
磁束密度とコイルの巻かれたコアの断面積の積よって磁束が決定します。磁束はΦ、コアの断面積はAeで表します。
4.磁束の変化と電圧の発生
コアの磁束が変化した時に、コアに巻かれたコイルには電圧が発生します。
それでは、いったん言葉と記号をまとめて1~4の関係を式で表してみます。
- 文字の定義
- H:磁界
- B:磁束密度
- μ:透磁率
- Φ:磁束
- Ae:コアの断面積
- N:巻き数

※(4)の表す意味:単位時間当たりの磁束の変化が大きいと、発生する電圧vも大きくなります。
※透磁率μ:(2)式の通り、透磁率μはB-H曲線の傾きとなります。
ここで、パルストランス設計におけるヒステリシス曲線(B-H曲線)の見方を説明します。
以下に、とあるコアのB-H曲線を示します。

横軸が磁界H,縦軸が磁束密度Bです。式(1)より、磁界Hはコイルに流れる電流Iに比例するため、HをIに置き換えて見ることも可能です。式(2)を見てください。磁界Hが増える(電流が増える)と磁束密度Bは上昇していきます。ですが、Bの上昇にも上限があります。これを飽和磁束密度と呼び、図でいうところのBsに当たります。
ここで、磁界H(コイルの電流)を上げて行き、Bs付近でトランスを使うとどうなるかについて説明します。
Bs付近の拡大画像

先ほど言いましたように、透磁率μはB-H曲線の傾きです。磁界Hが小さい(電流が小さい)ときの傾きは、画像左下のように透磁率μは大きな値をとります。この時、このコアは1次コイルの電気エネルギーを磁気エネルギーに変えて伝達することが可能です。
では、磁界Hが大きい(電流が大きい)ときはどうでしょうか?画像右上を見てください。透磁率μは大変小さな値をとります。すると、電気エネルギーを磁気エネルギーに変換することができず、2次コイルへ信号を伝達できません!
それどころか、透磁率μが大変小さいときの1次コイルは空芯コイルと同様です。ですから、1次コイルのインダクタンスが大変小さい値をとり、大電流が流れて素子を破壊してしまいます!
このように、Bが最大磁束密度Bsの状態になり、透磁率μが大変小さくなってしまうことを、磁気飽和を起こすと言います。トランスの設計において、磁気飽和を起こさないように設計することが大変重要です。
では、磁気飽和を起こさないように使うにはどうすればいいでしょうか?
答えは、B-H曲線上に記したΔBの範囲で使うことです。
ΔBmaxを最大動作磁束密度といい、正側のパルスの磁束密度はこちらの大きさまでにするとうまく動きます。(なぜなら、透磁率が小さすぎないためトランスとして動作する。)
*ΔBmaxはコアにもよりますが、フェライトですと300mTが妥当です。
パルストランスの設計
前回の記事で、パルストランスの巻き数の決定方法を紹介しました。
 それでは、こちらの式を導出してみましょう。
それでは、こちらの式を導出してみましょう。

まず、私たちが回路を設計した段階でわかっていることは、1次コイルに与えるパルスの電圧と周波数です。式(4)を「電圧の変化で磁束が発生」という風に置き換えるところからスタートします。


※式(9)をご覧ください。
コイルに入力するEとTの積がΔBを上回らないように定める必要があります。
ときたまET積という言葉を耳にしたことがあるかもしれませんが、それがこちらです。
パルストランスのデータシートに記載されるET積は実はコアのΔBmaxによって制限されているのですね!
以上のようにして式を導出しました。
それでは、実際にこの式を使ってトランスを設計してみようと思います。
今回使用したコアは
こちら

アキバの日米で売ってました。(コアとボビン合わせて200円くらいでした)
こちらの資料から、コア断面積Ae=161㎟であるとわかります。
B-H曲線がこちらです。

今回は余裕を見て、最大動作磁束密度ΔBmaxを320mTとしましょう。
これは、100°Cでもμの値(接線の傾き)が十分大きいところ、、としました。
今回は何も考えずにこちらのコアに1次に15回、2次に30回巻きました。
それでは、こちらのパルストランスが伝達できる最低周波数を求めます。


よって最低周波数が3.87kHzと求まりましたから、これが正しいかどうか計測してみましょう。
*最低周波数:(パルス電圧Eが決まっているとき)これ以上の周波数であればトランスが伝達可能なパルスの周波数。

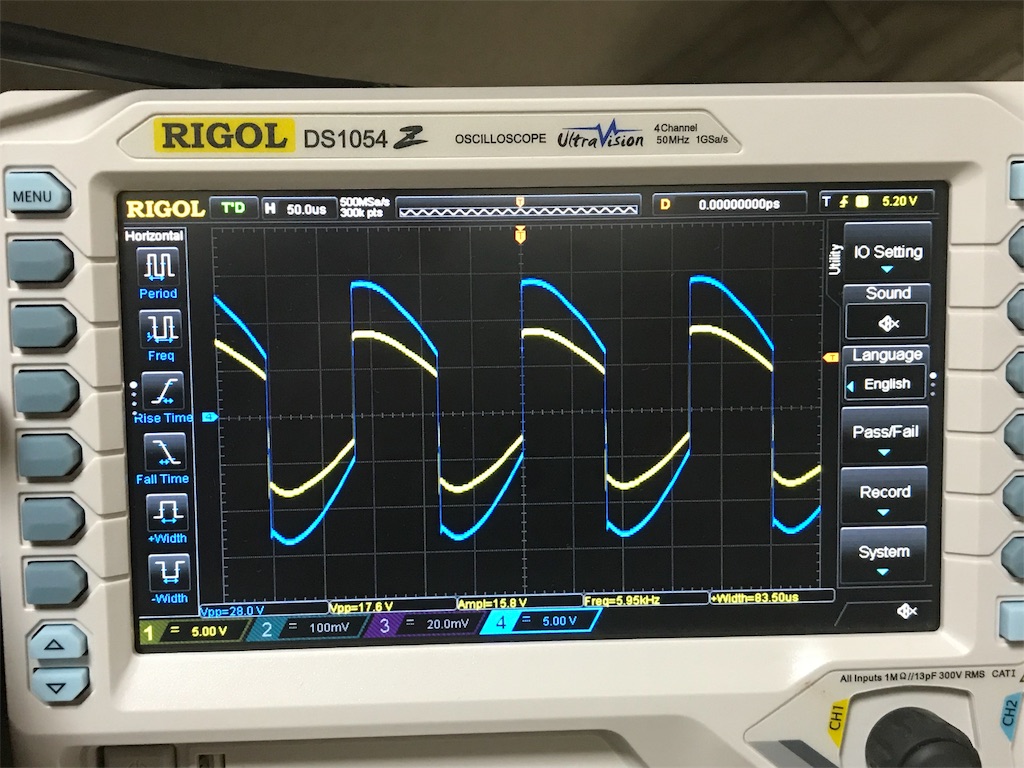
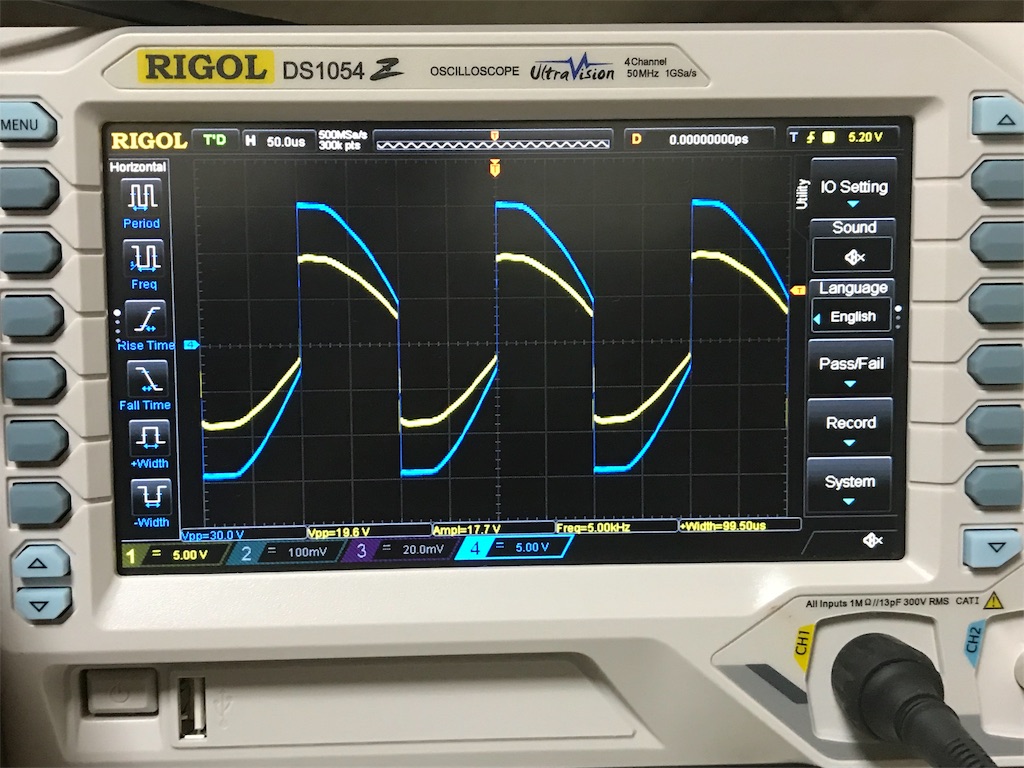
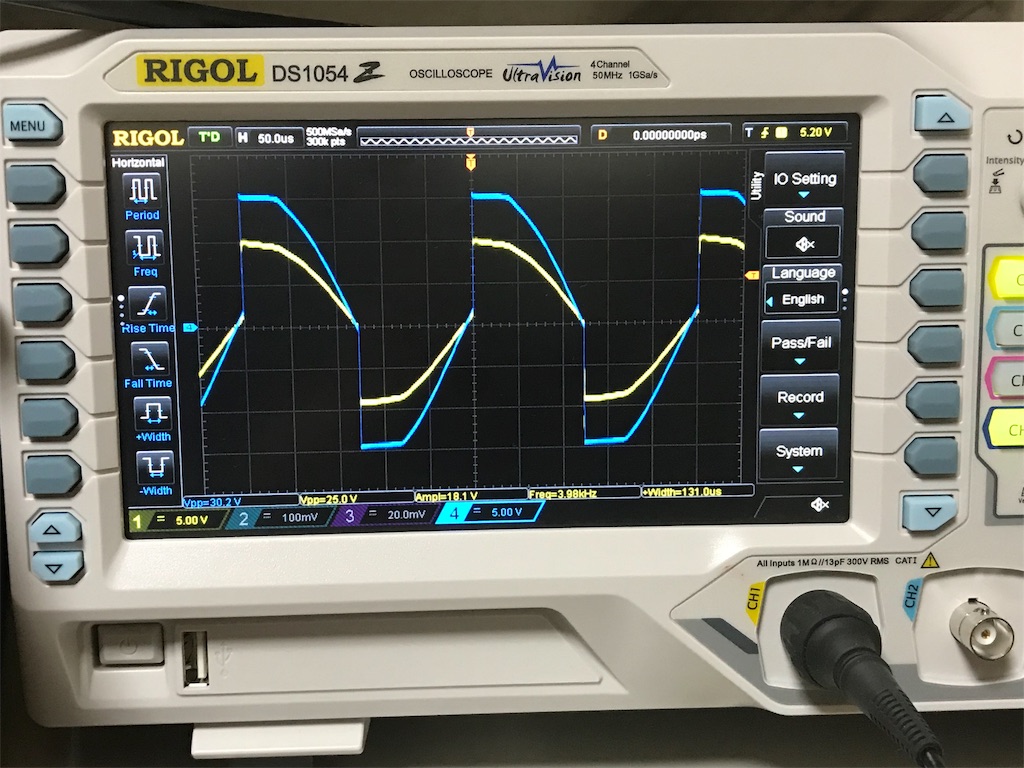
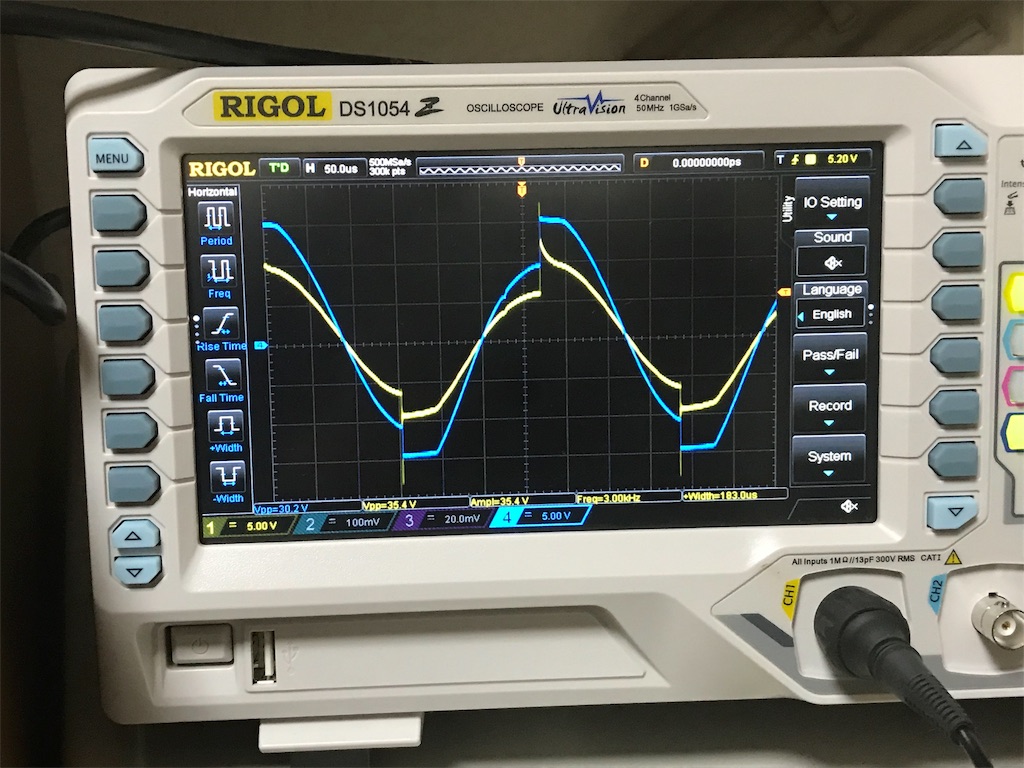
左から、6kHz-5kHz-4kHz-3kHz時の波形です。
黄色:1次コイルの電圧波形
青色:2次コイルの電圧波形
6~4kHzまではパルストランス として機能していますが、3kHz時はパルストランスとして機能していないことがわかります。
計算の結果がおおむね正しかったことが実証されました(ホッ)
また、2次コイルの電圧は1次コイルに比べてほぼ倍になっています。巻き数比に比例して誘導される電圧が変わることも確認できました。
追記:この測定結果からわかることですが、伝達可能な最低周波数(付近の周波数)の時の波形は大変汚いです。
矩形波には高調波が含まれるため、10倍程度の余裕を持って設計してもいいのでは?という意見も頂きました。皆様も作る際は十分に余裕を持った設計をよろしくお願いします。
追記:
記事製作時に残留磁束密度の概念がよくわかってなかったのでないがしろにしてましたが、本来であればET積による磁束密度の変化分ΔBが残留磁束密度Brに加わる形になるためBr+ΔB≦Bsとしなければなりませんでした。
内容は概ね合ってると思いますが、間違いが散見されるかもしれません。ご了承下さい。
なおフルブリッジ駆動のため正負に偏磁する事を考えると-Br+ΔB≦Bsとなりそうなので、この記事の上の式でやっても問題は無さそうです。
おわりに
今回はパルストランス、GDTの設計について細かく触れました。
多少計算をごまかしているところもありますが、直感的に理解できる内容になっているのではないかと思います。
みんなも作ろう、Letsパルストランス!
参考文献
http://hirachi.cocolog-nifty.com/kh/files/20100930-1.pdf
参考資料
https://product.tdk.com/info/ja/catalog/datasheets/ferrite_mz_large_pq_ja.pdf
https://product.tdk.com/info/ja/catalog/datasheets/ferrite_mn-zn_material_characteristics_ja.pdf