ソフィア祭
こんばんは。ついに学祭の季節ですね。そんなわけで学祭に向けてテスラコイルをパワーアップさせました。
Super Mario pic.twitter.com/2qGdiOjfEJ
— 上智大学エレクトロニクスラボ (@Sophia_ele_lab) October 30, 2018
よさみカメラを部員が持っていたのでそちらで撮影したところ素晴らしい放電が取れました。フォトジェニックですね。ツイッタでも院スタでも映えるテスラは最高の被写体だと思いますハイ。
そんなわけでこちらのテスラを学祭で展示します。

時・ところ
上智大学四谷キャンパス 紀尾井101教室
11/2~11/4 10:00~16:00
(画像では107となっていますが101に変更となりました。お気をつけください)
ついでに2重奏もやってみました。
スプラッシュマウンテン...!
— 上智大学エレクトロニクスラボ (@Sophia_ele_lab) October 26, 2018
11/2〜4の学祭で見られます!! pic.twitter.com/ozqmrvLclA
アルミ線ぐるぐるトロイドを付けたら放電伸びたんですけど1次と放電して基板ごと逝きました()
よって2重奏はできなそうです(つらい)。
ついでに爆音テスラの横でプログラミング教室もやるようです。
— 上智大学エレクトロニクスラボ (@Sophia_ele_lab) October 31, 2018
最大収容人数20人の部屋でできるんでしょうか?
さすがにまずいと思います。
テスラでPCバグりそう
でも安心してください!
なんとPCはアキバのジャンク品!!
こちらでご用意します。
しかもプログラミング教室中は放電しないっぽいです!!!!!
あたりまえですね。
VVVFもいい感じにできたら展示します。あと一日で何とかなるのでしょうか…
そんなわけで不安が残ったまま学祭期間に突入しますが、ぜひソフィ大に遊びに来てください!
パルストランス(GDT)の設計
こんにちはkentamuです。前回の記事で触れたパルストランス(GDT、ゲートドライブトランス)の設計方法を紹介します。
そもそもトランスって?
トランスとはトランスフォーマー(変圧器)のことで、高磁性体(磁化されやすい)コアにコイルがまかれたような構造をしています。
プラスチックのボビンにコイルがまかれる様子

フェライトのコアをボビンの上下からサンドイッチして完成したトランス

トランスの解体図。左から、フェライトコア、ボビン、フェライトコア。

回路図は以下の通りです。
T1の文字の下にある2本線がコアを示し、コイルに打ってある・(ドット)が巻き始めを意味します。下の回路図ですと、同じコアに3つのコイルが巻かれていることになります。

信号が入力されるコイルを1次コイル、信号が伝達される側のコイルを2次コイルといいます。回路図ですと、1-2が1次、3-4,5-6が2次コイルです。
では、どやって信号を伝達しているのでしょうか?
答えは簡単です。コアの持つ磁気エネルギーを利用しています。
まず、1次コイルに入った電気エネルギーにより、コアに磁気エネルギーが発生します。そして、同じコアにまかれた2次コイルに磁気エネルギーの影響で電気エネルギーが発生します。
電気エネルギー → 磁気エネルギー → 電気エネルギー
このような順番でエネルギーが伝達されます。
つまり、トランスは電気的に絶縁しながら信号を伝達してくれるパーツとなります。
トランスの動作とB-H曲線
電子工作をしていると、時々目にするのがヒステリシス曲線(B-H曲線)です。
本項ではヒステリシス曲線について、トランスの動作を交えながら考えていきます。

トランスの動作
1.電流と磁界
コイルがまかれているとき、コイルに電流が流れると磁界が発生します。これが磁気エネルギーの発端です。磁界はHで表します
2.磁界と磁束密度
コアにコイルがまかれていて磁界が発生すると、コアの透磁率(磁界の通しやすさ)に比例して、磁束密度というものが決定します。透磁率はμ、磁束密度はBで表します。コアは空気よりも透磁率がとても大きいですから、空芯コイルよりも大きな磁束密度を持たせることができます。
3.磁束密度と磁束
磁束密度とコイルの巻かれたコアの断面積の積よって磁束が決定します。磁束はΦ、コアの断面積はAeで表します。
4.磁束の変化と電圧の発生
コアの磁束が変化した時に、コアに巻かれたコイルには電圧が発生します。
それでは、いったん言葉と記号をまとめて1~4の関係を式で表してみます。
- 文字の定義
- H:磁界
- B:磁束密度
- μ:透磁率
- Φ:磁束
- Ae:コアの断面積
- N:巻き数

※(4)の表す意味:単位時間当たりの磁束の変化が大きいと、発生する電圧vも大きくなります。
※透磁率μ:(2)式の通り、透磁率μはB-H曲線の傾きとなります。
ここで、パルストランス設計におけるヒステリシス曲線(B-H曲線)の見方を説明します。
以下に、とあるコアのB-H曲線を示します。

横軸が磁界H,縦軸が磁束密度Bです。式(1)より、磁界Hはコイルに流れる電流Iに比例するため、HをIに置き換えて見ることも可能です。式(2)を見てください。磁界Hが増える(電流が増える)と磁束密度Bは上昇していきます。ですが、Bの上昇にも上限があります。これを飽和磁束密度と呼び、図でいうところのBsに当たります。
ここで、磁界H(コイルの電流)を上げて行き、Bs付近でトランスを使うとどうなるかについて説明します。
Bs付近の拡大画像

先ほど言いましたように、透磁率μはB-H曲線の傾きです。磁界Hが小さい(電流が小さい)ときの傾きは、画像左下のように透磁率μは大きな値をとります。この時、このコアは1次コイルの電気エネルギーを磁気エネルギーに変えて伝達することが可能です。
では、磁界Hが大きい(電流が大きい)ときはどうでしょうか?画像右上を見てください。透磁率μは大変小さな値をとります。すると、電気エネルギーを磁気エネルギーに変換することができず、2次コイルへ信号を伝達できません!
それどころか、透磁率μが大変小さいときの1次コイルは空芯コイルと同様です。ですから、1次コイルのインダクタンスが大変小さい値をとり、大電流が流れて素子を破壊してしまいます!
このように、Bが最大磁束密度Bsの状態になり、透磁率μが大変小さくなってしまうことを、磁気飽和を起こすと言います。トランスの設計において、磁気飽和を起こさないように設計することが大変重要です。
では、磁気飽和を起こさないように使うにはどうすればいいでしょうか?
答えは、B-H曲線上に記したΔBの範囲で使うことです。
ΔBmaxを最大動作磁束密度といい、正側のパルスの磁束密度はこちらの大きさまでにするとうまく動きます。(なぜなら、透磁率が小さすぎないためトランスとして動作する。)
*ΔBmaxはコアにもよりますが、フェライトですと300mTが妥当です。
パルストランスの設計
前回の記事で、パルストランスの巻き数の決定方法を紹介しました。
 それでは、こちらの式を導出してみましょう。
それでは、こちらの式を導出してみましょう。

まず、私たちが回路を設計した段階でわかっていることは、1次コイルに与えるパルスの電圧と周波数です。式(4)を「電圧の変化で磁束が発生」という風に置き換えるところからスタートします。


※式(9)をご覧ください。
コイルに入力するEとTの積がΔBを上回らないように定める必要があります。
ときたまET積という言葉を耳にしたことがあるかもしれませんが、それがこちらです。
パルストランスのデータシートに記載されるET積は実はコアのΔBmaxによって制限されているのですね!
以上のようにして式を導出しました。
それでは、実際にこの式を使ってトランスを設計してみようと思います。
今回使用したコアは
こちら

アキバの日米で売ってました。(コアとボビン合わせて200円くらいでした)
こちらの資料から、コア断面積Ae=161㎟であるとわかります。
B-H曲線がこちらです。

今回は余裕を見て、最大動作磁束密度ΔBmaxを320mTとしましょう。
これは、100°Cでもμの値(接線の傾き)が十分大きいところ、、としました。
今回は何も考えずにこちらのコアに1次に15回、2次に30回巻きました。
それでは、こちらのパルストランスが伝達できる最低周波数を求めます。


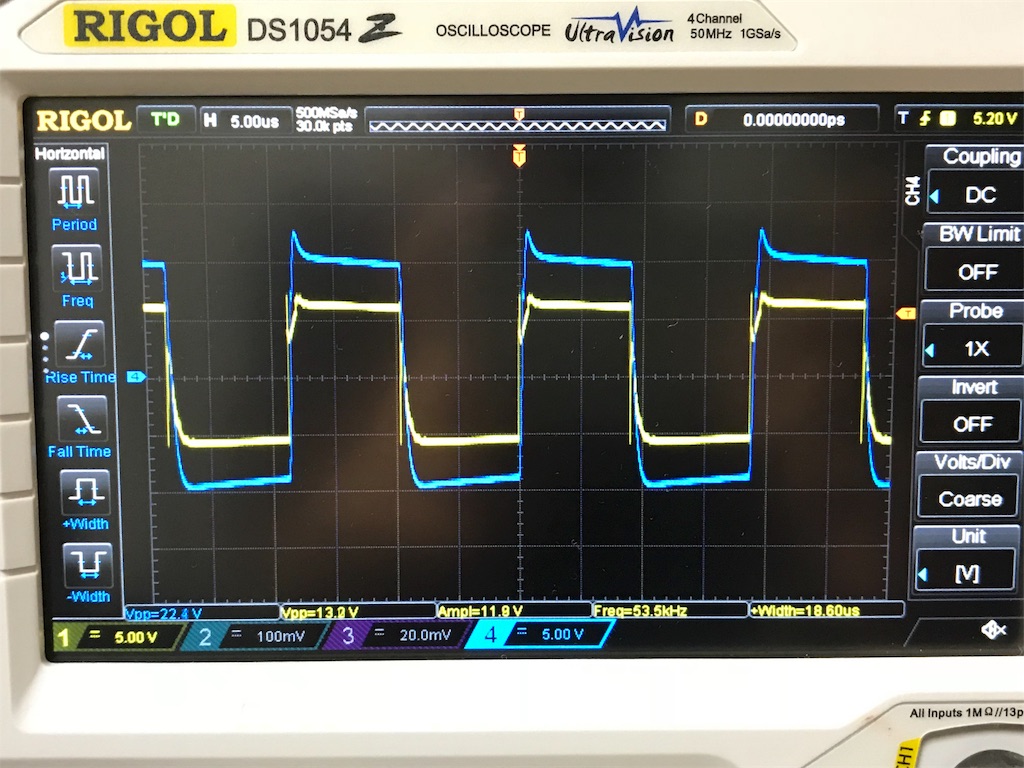
よって最低周波数が3.87kHzと求まりましたから、これが正しいかどうか計測してみましょう。
*最低周波数:(パルス電圧Eが決まっているとき)これ以上の周波数であればトランスが伝達可能なパルスの周波数。

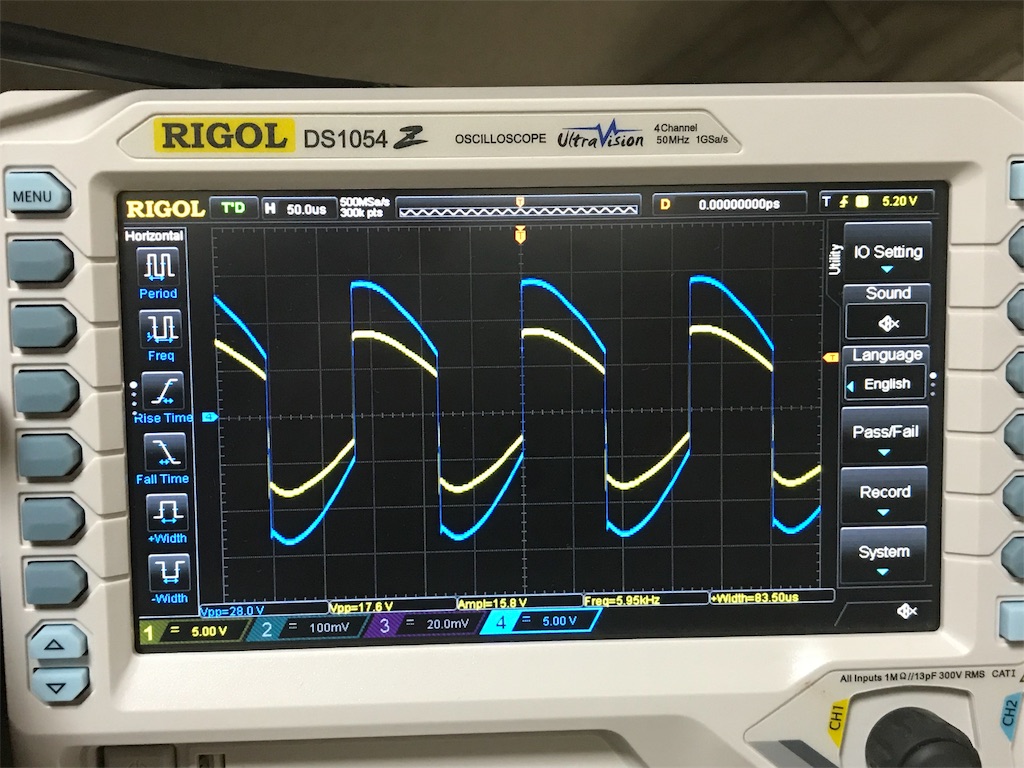
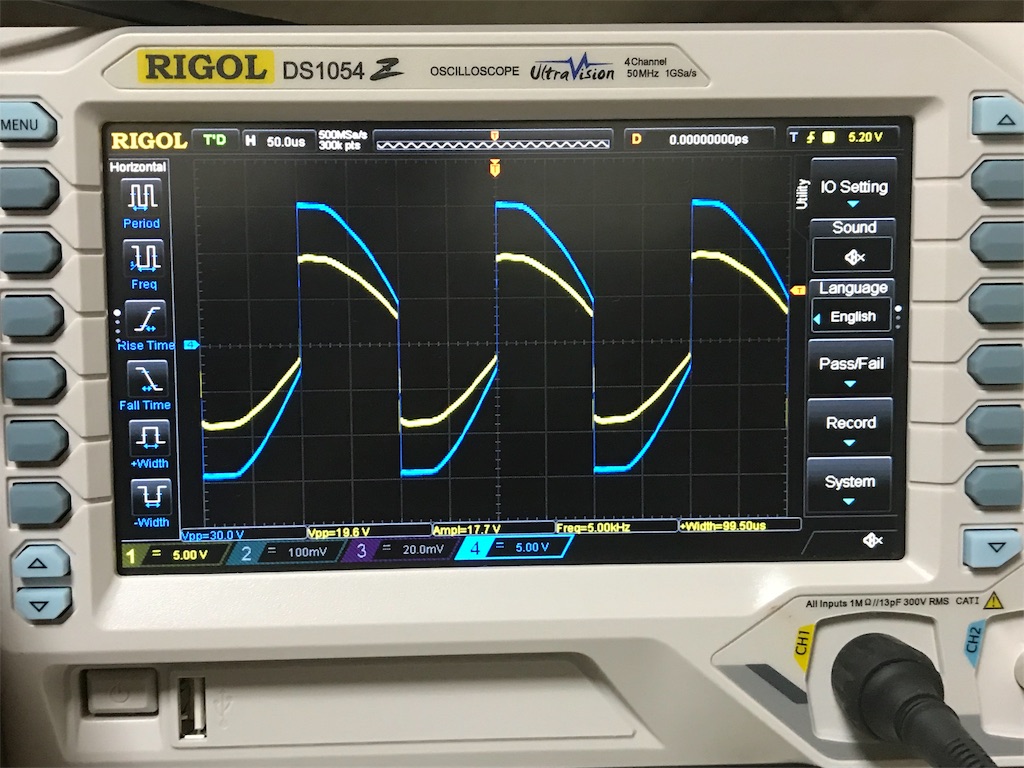
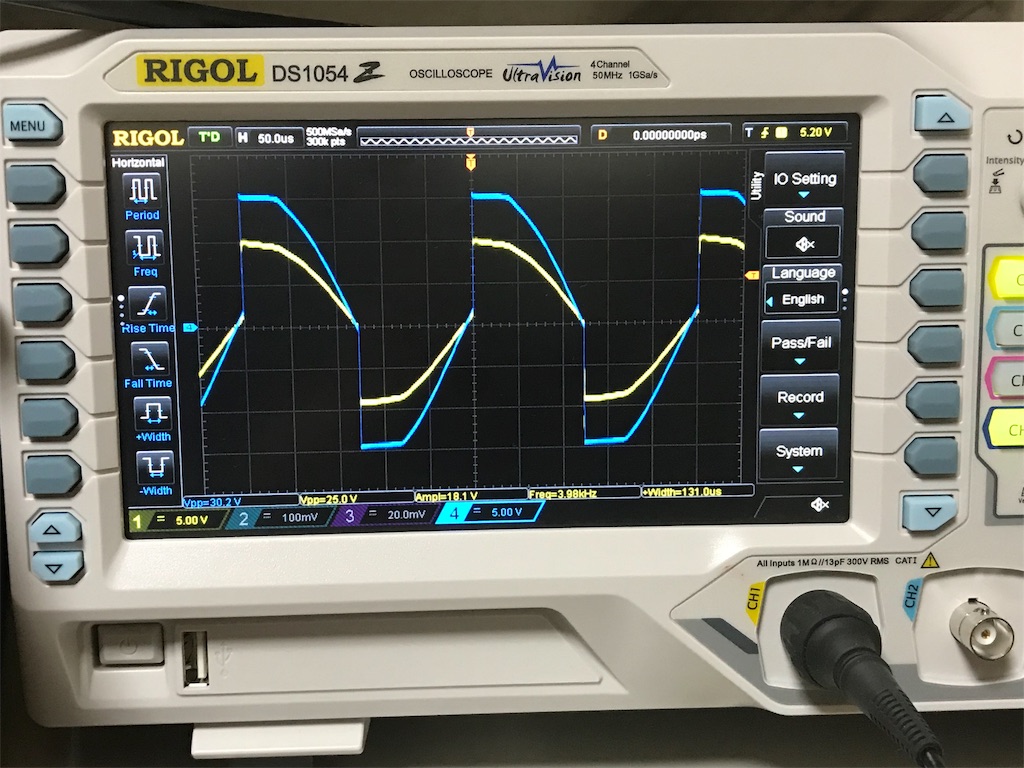
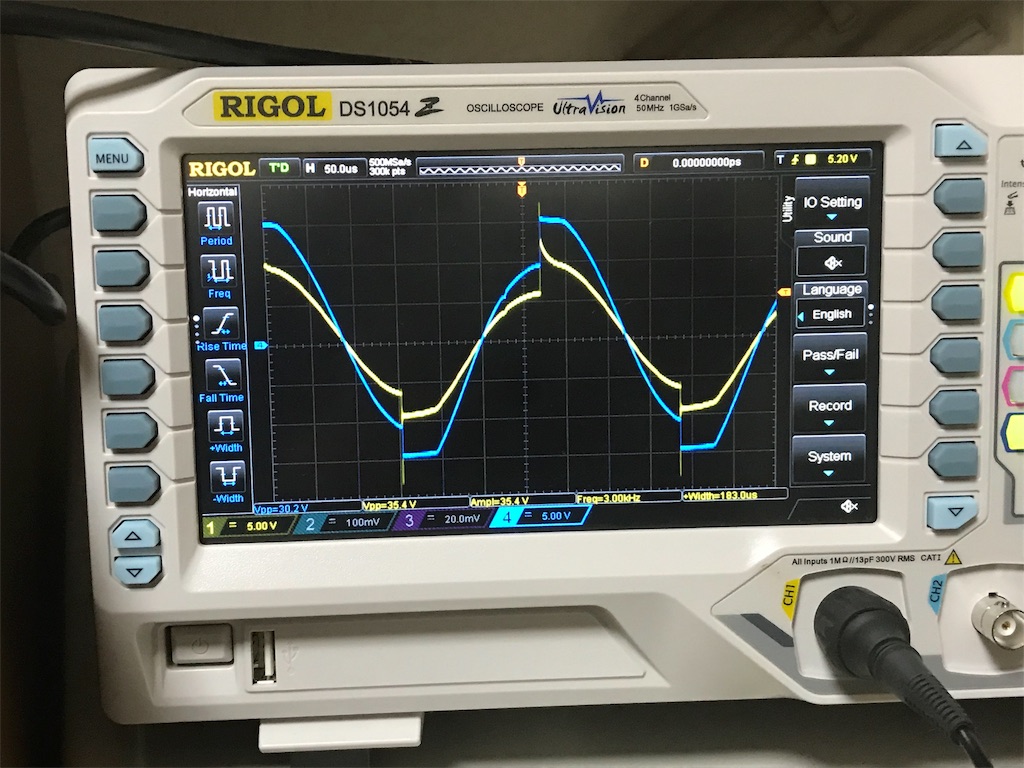
左から、6kHz-5kHz-4kHz-3kHz時の波形です。
黄色:1次コイルの電圧波形
青色:2次コイルの電圧波形
6~4kHzまではパルストランス として機能していますが、3kHz時はパルストランスとして機能していないことがわかります。
計算の結果がおおむね正しかったことが実証されました(ホッ)
また、2次コイルの電圧は1次コイルに比べてほぼ倍になっています。巻き数比に比例して誘導される電圧が変わることも確認できました。
追記:この測定結果からわかることですが、伝達可能な最低周波数(付近の周波数)の時の波形は大変汚いです。
矩形波には高調波が含まれるため、10倍程度の余裕を持って設計してもいいのでは?という意見も頂きました。皆様も作る際は十分に余裕を持った設計をよろしくお願いします。
追記:
記事製作時に残留磁束密度の概念がよくわかってなかったのでないがしろにしてましたが、本来であればET積による磁束密度の変化分ΔBが残留磁束密度Brに加わる形になるためBr+ΔB≦Bsとしなければなりませんでした。
内容は概ね合ってると思いますが、間違いが散見されるかもしれません。ご了承下さい。
なおフルブリッジ駆動のため正負に偏磁する事を考えると-Br+ΔB≦Bsとなりそうなので、この記事の上の式でやっても問題は無さそうです。
おわりに
今回はパルストランス、GDTの設計について細かく触れました。
多少計算をごまかしているところもありますが、直感的に理解できる内容になっているのではないかと思います。
みんなも作ろう、Letsパルストランス!
参考文献
http://hirachi.cocolog-nifty.com/kh/files/20100930-1.pdf
参考資料
https://product.tdk.com/info/ja/catalog/datasheets/ferrite_mz_large_pq_ja.pdf
https://product.tdk.com/info/ja/catalog/datasheets/ferrite_mn-zn_material_characteristics_ja.pdf
テスラコイルの回路
こんにちはkentamuです。前回紹介したテスラコイルの回路について詳しく見てみようと思います。
回路図
*クリックで拡大します

*高解像度版をアップしました
テスラコイルの回路図(高解像度) pic.twitter.com/Nj75kepwa9
— 上智大学エレクトロニクスラボ (@Sophia_ele_lab) September 24, 2018
では、この回路を分解してみてみましょう。
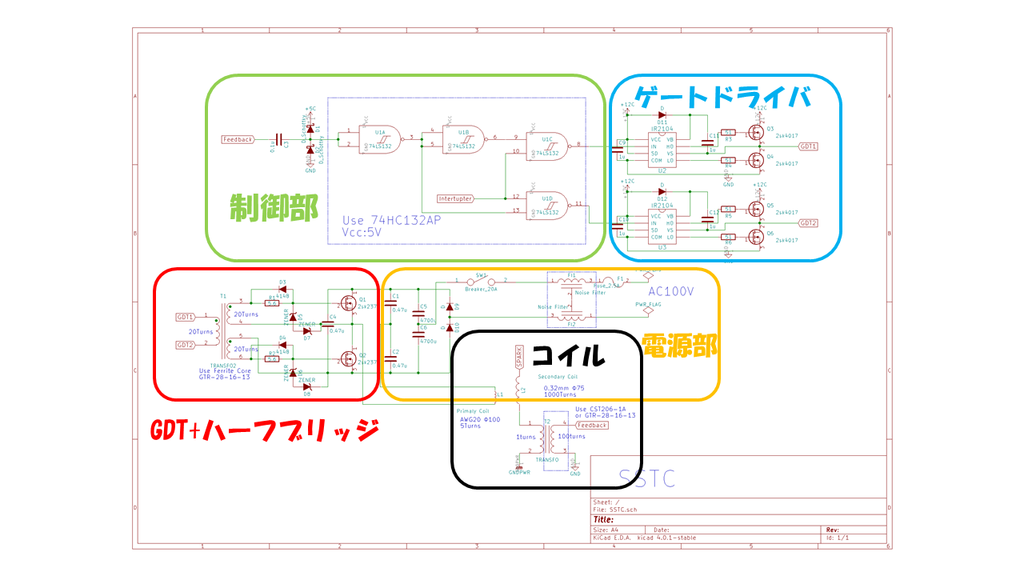
大きく分けると大体上のような感じです。
1つづつ見てみましょう。
コイル
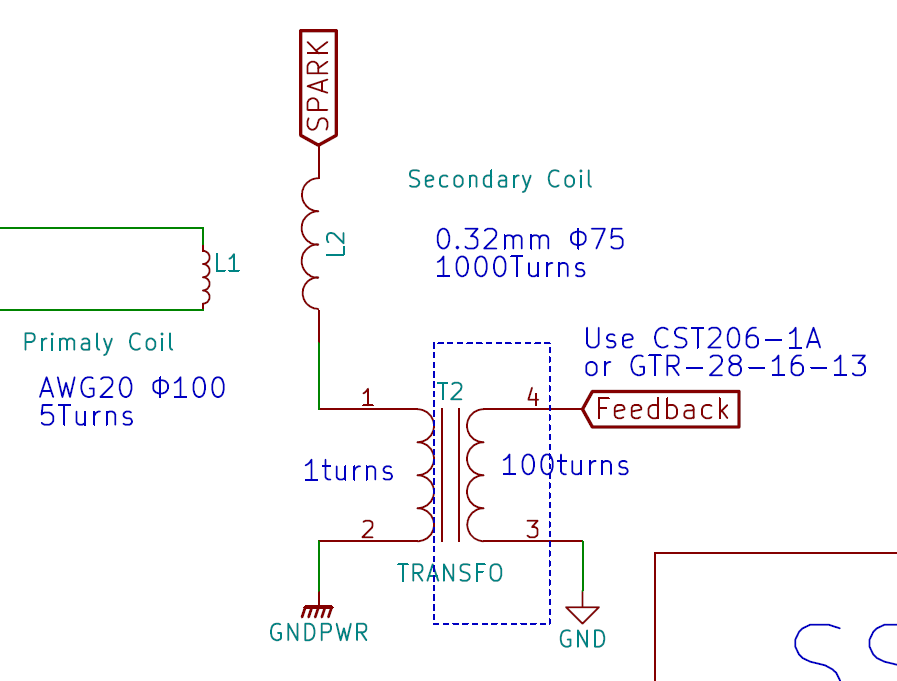
コイル部は適当です(棒)
2次コイルは以下のようにキャスターを使ってまくと非常に楽です。



2次コイルの放電が1次コイルに行くを防ぐために、1次コイルは2次コイルよりも太い塩ビパイプにま巻かれています。

テスラコイルの放電の原理はLC共振です。(諸説アリ?)2次コイルと2次コイルと空気の間に形成されるキャパシタンスによって共振周波数が決まります。
1次コイルへ2次コイルの共振周波数に合わせた周波数の大電力信号が入ると、2次コイルには共振周波数の電流が流れ、電流に比例した起電力をもち、とても高い電圧が発生してすんごい放電します。
共振周波数が固定だったらいいのですが、空気とコイルによって形成されるキャパシタンスは大変不安定です。もちろんキャパシタンスが変動すると共振周波数も変化しますので、その時々の共振周波数がわかるような仕組みがないと共振周波数でパルスを与えることができず、放電させられません!
そこで、2次コイルの共振周波数を検知する測定器、カレントトランス(CT・変流器)をつけます。
回路図右下にあるT2がCTとなります。
80回くらい巻きました。この穴に2次コイルのGND側を1回通します。
このコイルが2次コイルに流れる電流を検知して、制御回路へと入力されます。
CTによって得られる制御回路への信号を、フィードバック信号と呼びます。
*CTには向きがございます。放電しなかったときはCTや1次コイルの向きを変えてみましょう。

制御部
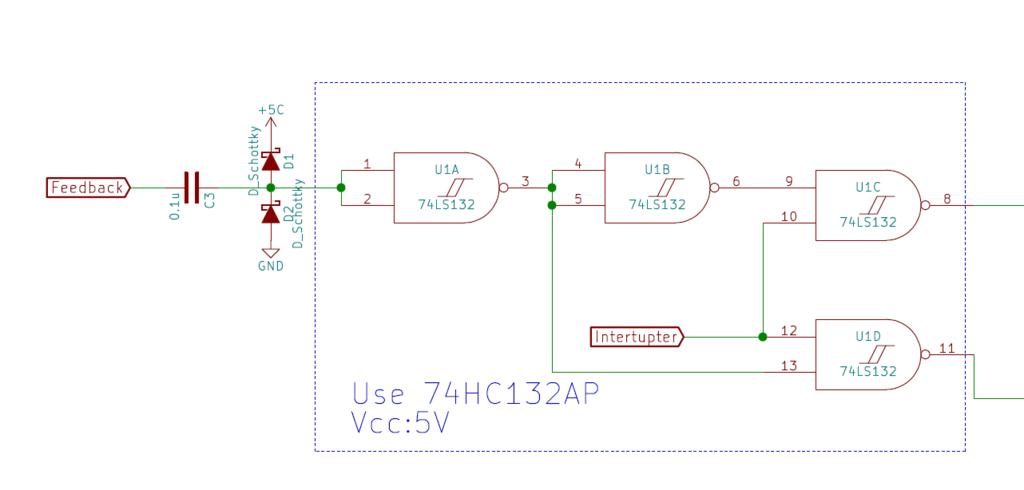
制御部はCTによるフィードバック信号をインタラプタ信号で変調しています。
つまり、2次コイルの共振周波数であるフィードバック信号と音源となるインタラプタ信号を乗算したような波形が出力されます。
U1AとU1BはNOTに置き換えられます。(デジタル回路ではNOTをインバータと表記することがあります。)
回路シュミレータLTSPICEでの波形解析結果をみてみましょう。
緑色がフィードバック信号、青色がインタラプタ信号だと思ってください。↓
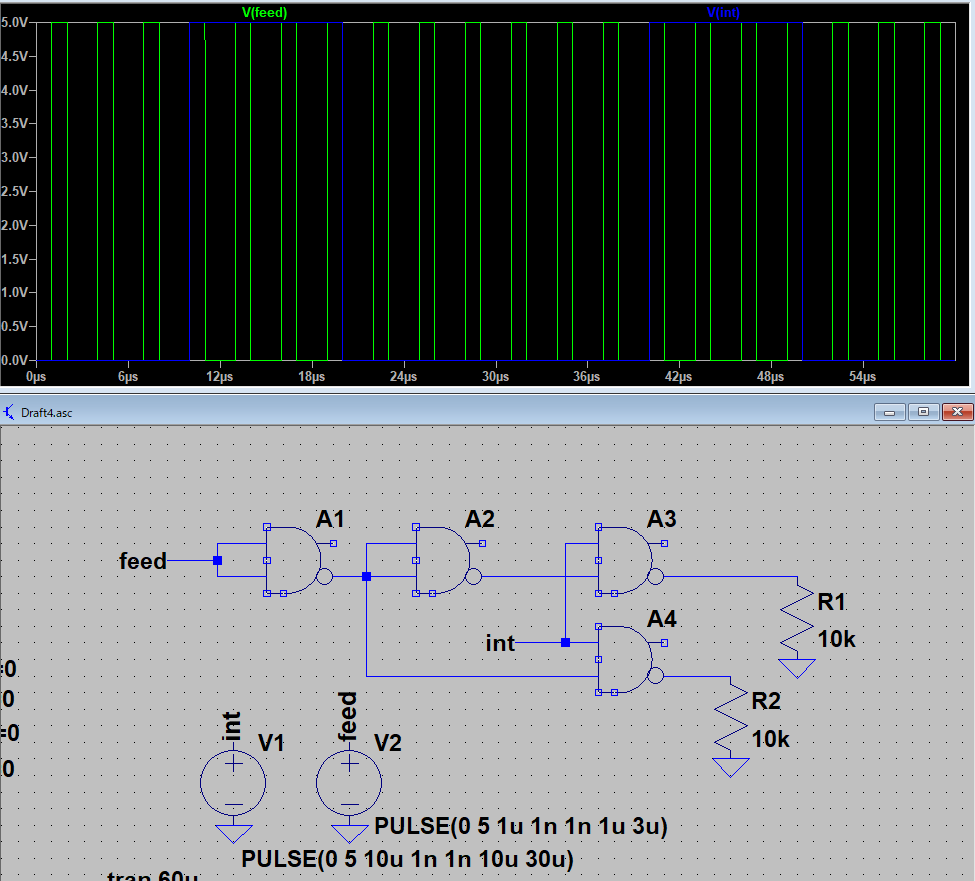
この信号が回路を通ると、R1にはフィードバック信号とインタラプタ信号の乗算回路の否定、R2はフィードバック信号の否定とインタラプタ信号の乗算回路の否定が出力されます。幅の短い信号が幅の広い信号に削り取られたような感じです。
R1の電圧が緑、R2の電圧が青です。↓
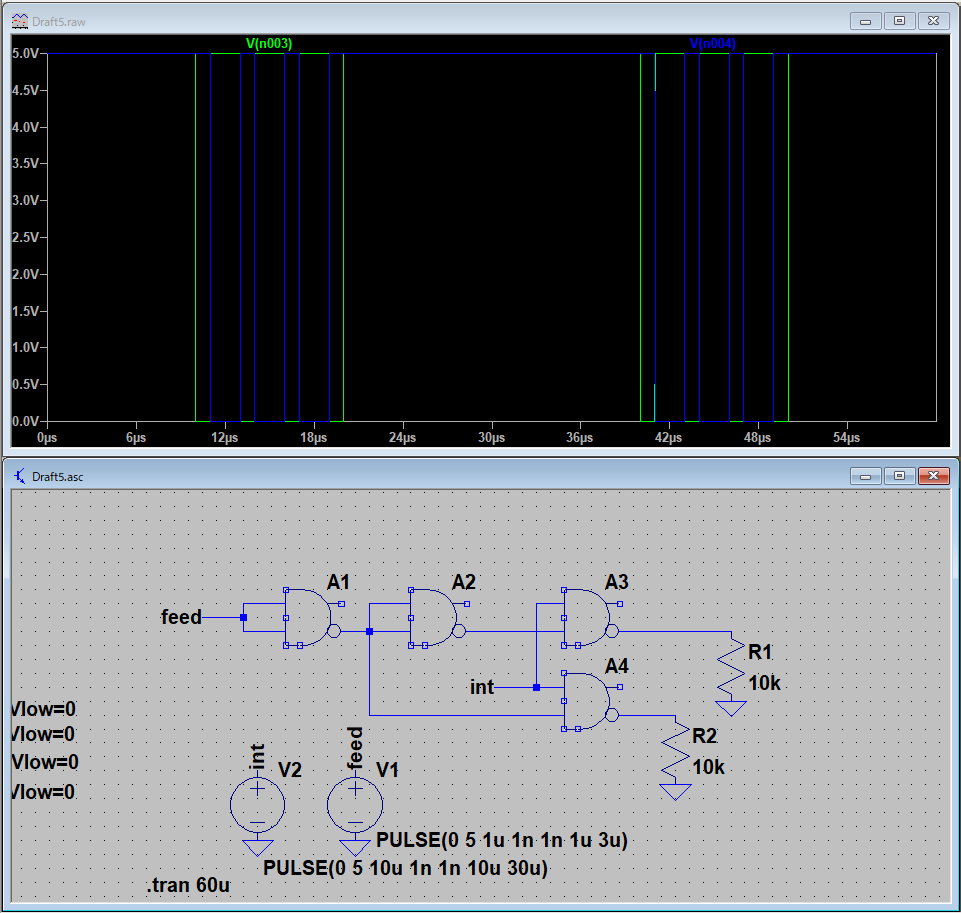
この2信号が制御部の出力信号となります。
*フィードバック信号の発生と周辺回路
ここで疑問になるのがフィードバック信号がどのように発生するかです。
最初2次コイルには電流が流れていないので共振周波数が電流波形としてCTから検出されることはございません。
そこでまず、インタラプタ信号によって信号を与えます。すると、ある周波数になった瞬間に共振を起こすため2次コイルへ大電流が流れます。
そしてその電流をCTで検知してフィードバック信号として制御基板にぶち込む感じです。
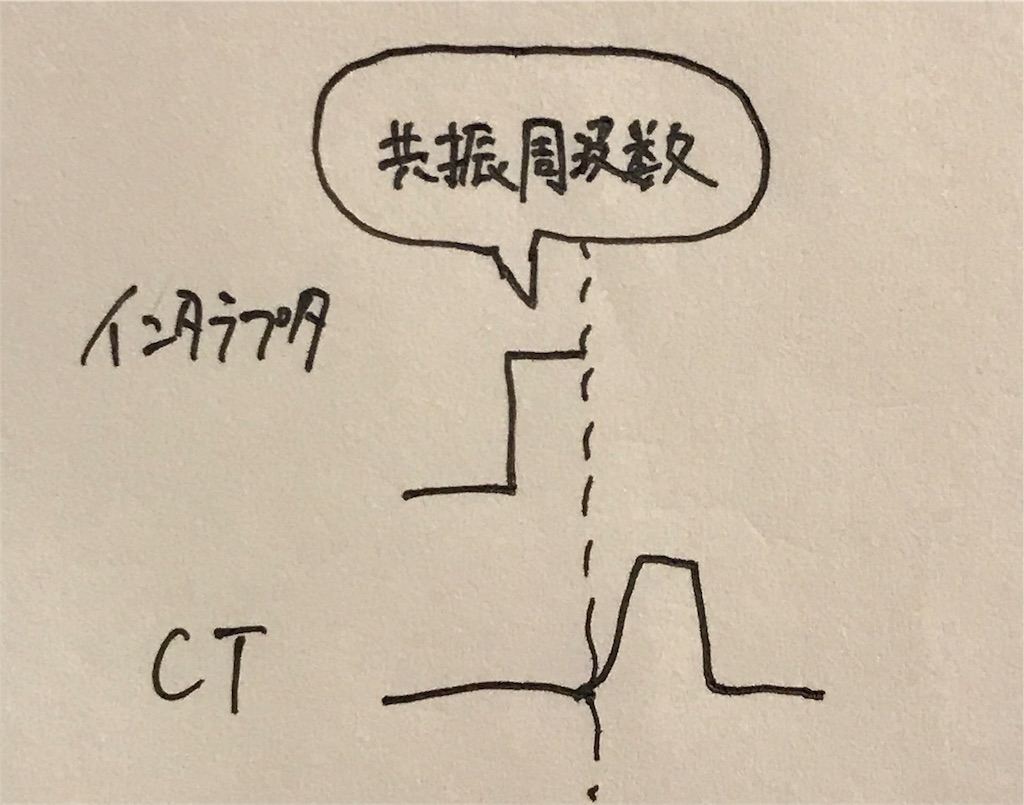
ここからは憶測で話します。間違ってたらすみません。間違いに気づいたらご指摘いただけると大変助かります。
CTによって電流を検知すると、誘導起電力としてCTにまいたコイルの両端には電圧が発生します。この電圧をD1.D2によってクランプするわけですが…
多分これがフィードバック信号の位相をいい感じにしてくれるんだと思います。
フィードバック信号と位相についてだれか教えて(えぇ…
ゲートドライバ
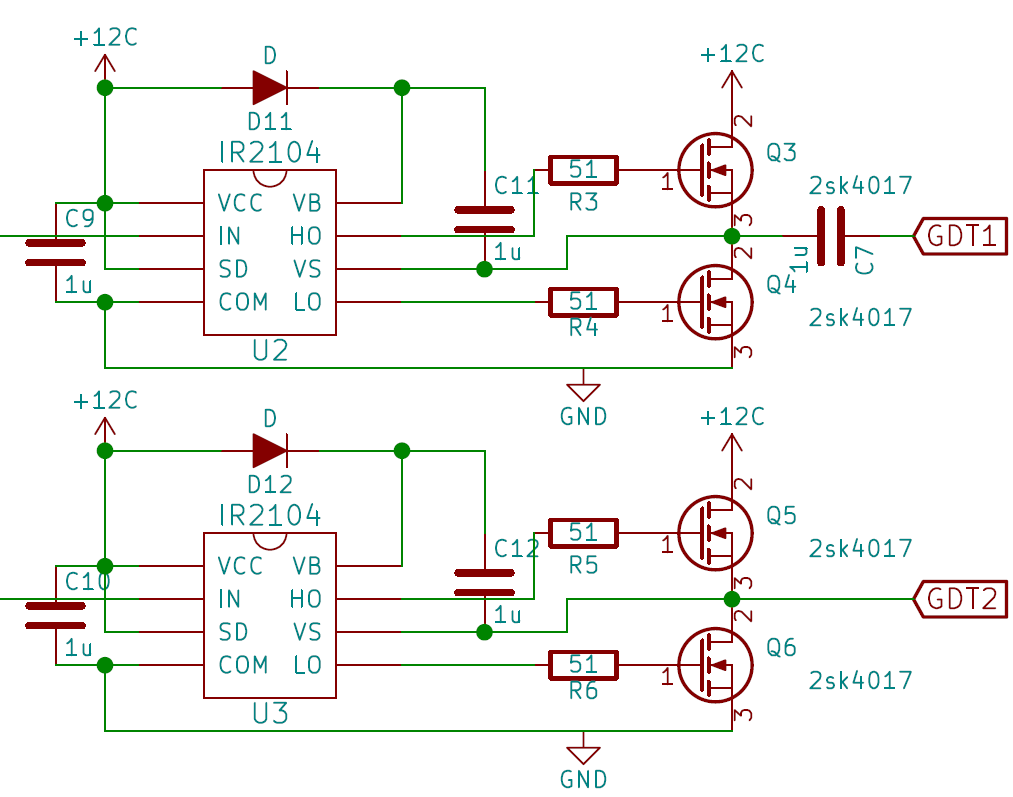
制御部から出力された信号がゲートドライバへとつながっています。今回はゲートドライバの最大出力を5Aとして、IGBTモジュールなどゲート容量の大きい素子も駆動出来るようにしました。
こちらの回路はGDTを駆動するために、上下に配置したハーフブリッジ回路2つを交互にOn/Offして大きめの電流を得ています。(フルブリッジ回路)
このフルブリッジ回路は、Q3,Q6を同時にONしてGDTに順バイアス、その後Q4,Q5を同時にONして逆バイアスをかけています。
フルブリッジ回路でGDTを駆動すると、GDTの両端電圧が等しくなる(ハーフブリッジの中点電位となる)ので、GDTの1次コイルには±6Vのパルスが印加されることになります。
ここでポイントとなるのが上側の回路の出力にあるC7です。
こちらはトランスフルブリッジ回路で駆動した際に起きてしまいがちな嫌な現象、「偏磁」を防ぐためのものです。簡単に説明します。
【偏磁】
偏磁とは、トランスのコアが偏った一方向に磁化されてしまうことです。
トランスの1次コイルに電圧をかけると磁束を作るために電流が発生します。これを励磁電流といいます。励磁電流とコイルへかける電圧には比例の関係があります。
通常順方向の励磁電流と逆方向の励磁電流にはイコールの関係がありバランスが取れています。
何らかの原因で順方向励磁電流と逆方向励磁電流のバランスが崩れると、徐々に片方の電流が大きくなるり、コアが一方向に磁化します。
そうしますと、、トランスが磁気飽和を起こして結果的に1次コイルのインダクタンスが下がり、電流がめちゃ流れやすくなって1次コイルに流す電流が過電流となりゲートドライバの定格を上回りFETを破壊します。
以上が偏磁とその影響です。怖いですね。そこで、こちらのコンデンサC7がうまく機能してくれます。
【偏磁防止コンデンサの役割】
このコンデンサは一方向の電流の増大によってコンデンサの両端に電圧を発生させます。すると1次コイルにかかる電圧がコンデンサの両端電圧の分だけ変化します。この変化によって比例の関係にある励磁電流も変化し、いい感じに順方向励磁電流と逆方向励磁電流のバランスがとれるという寸法です。
大変長ったらしい説明でごめんなさい。
こちらが私が参考にした資料です。ぜひご覧になってください。
・偏磁のメカニズム
http://hirachi.cocolog-nifty.com/kh/files/20111101-1.pdf
・偏磁防止用のコンデンサの動作
http://hirachi.cocolog-nifty.com/kh/files/20160901-1.pdf
それでは実際の入力波形と、出力波形であるGDT1-GDT2の波形を見てみましょう。
入力波形:上がフィードバック信号で、下がインタラプタ信号だと思てください。(オシレーターで作った擬似波形です。)
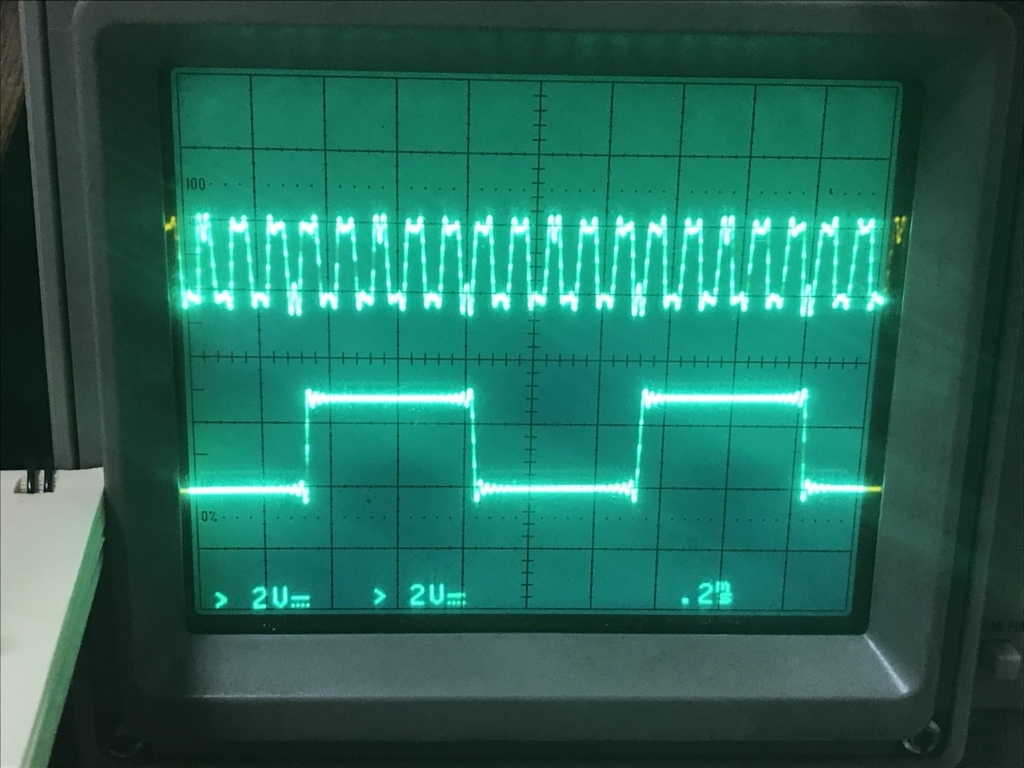
出力波形(GDT1-GDT2波形):インタラプタ信号でフィードバック信号がきれいに乗算され、±6Vに振れているのがわかります。

上の画像の波形がGDTの1次コイルへと入力されます。
GDT+ハーフブリッジ部
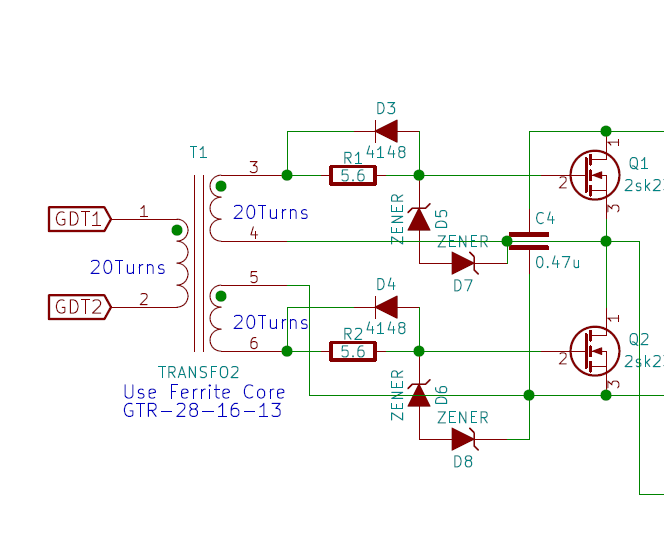
前項のフルブリッジによって駆動していたのがこちらのトランス、GDTでございます。このGDTがQ1,Q2(ハーフブリッジ)のゲートを駆動します。
GDT巻き数比が1:1:1ですから、1次コイルを±6Vで駆動しているため2次コイルにもそれぞれ±6Vが出力されます。
実はこれがあまりよくなくて、パワーMOSFETのゲート駆動には±15Vが最適な場合が多く、±6Vだとちょっと電圧不足です。そこで後から1次コイルを15回巻、2次コイルを30回巻としたところ、なかなかいい感じに昇圧してくれました。
黄色が1次コイルの電圧、青色が2次コイルの電圧です。ちゃんと昇圧されてますね!
2次コイルの波形にちょっとピョコっとしたサージ電圧(オーバーシュート)が確認できます。サージ電圧を抑える方法として、ゲートに直列につながっている抵抗(ゲート抵抗)を大きくする方法があります。ゲート抵抗を変更したらオシロで確認し、波形の見た目の気が済むまで抵抗をとっかえひっかえしましょう。私はこれで気が済んだのでそのままです。
ゲート抵抗と並列に入っているダイオードはデッドタイム確保用のものですが、GDTが勝手にデッドタイムを作ってくれるのでなくても大丈夫です。一応入れました。
ゲート-エミッタ間についているのツェナーダイオード(ZD)は、G-E間電圧が定格の±15Vを超えないようにするためのものです。万が一ノイズが乗ってFETのG-E間電圧の定格を超えてしまっては大変です。ZDのカソード、またはアノードを向かい合わせにして挿入することで正負の電圧を降伏電圧までの大きさにしてくれます。
*ここからはGDTの設計方法を紹介します。
今回は2次コイルの共振周波数、使用するトランスのコアがわかっているものとします。
以下が今回の回路方式におけるパルストランスの巻き数の計算式です。
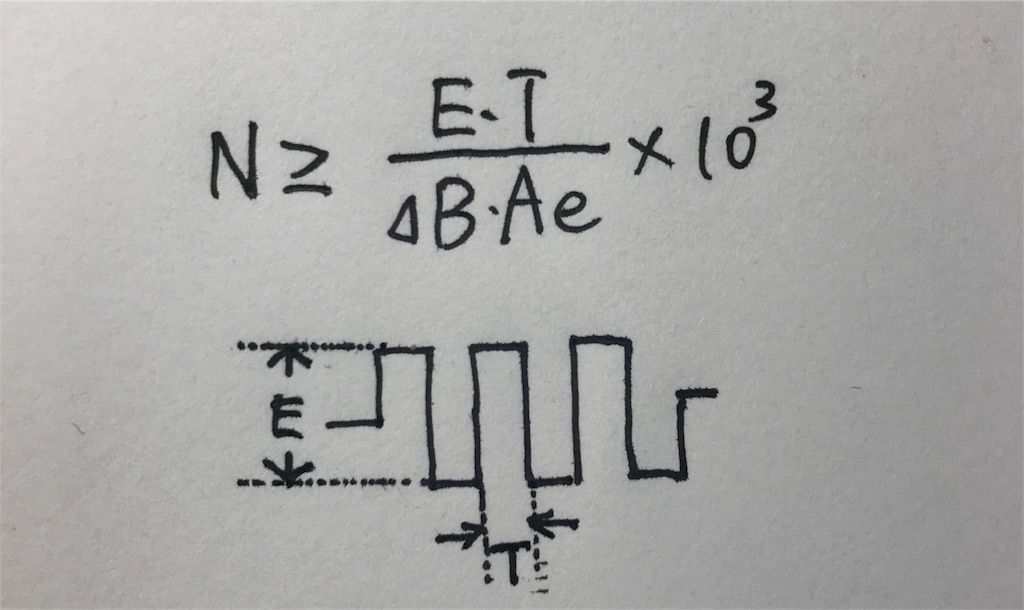
- N:巻き数(回)
- E:パルス電圧(V)
- T:On時間(μS)
- ΔB:飽和磁束密度(mT)
- Ae:コア断面積(㎟)
*Tについて
TパルスがOnしている時間(上図)なので(矩形波の周期/2)となり、(1/(共振周波数・2))です。余裕をもって、共振周波数は実測の共振周波数-10kHzくらいに設定してみましょう。
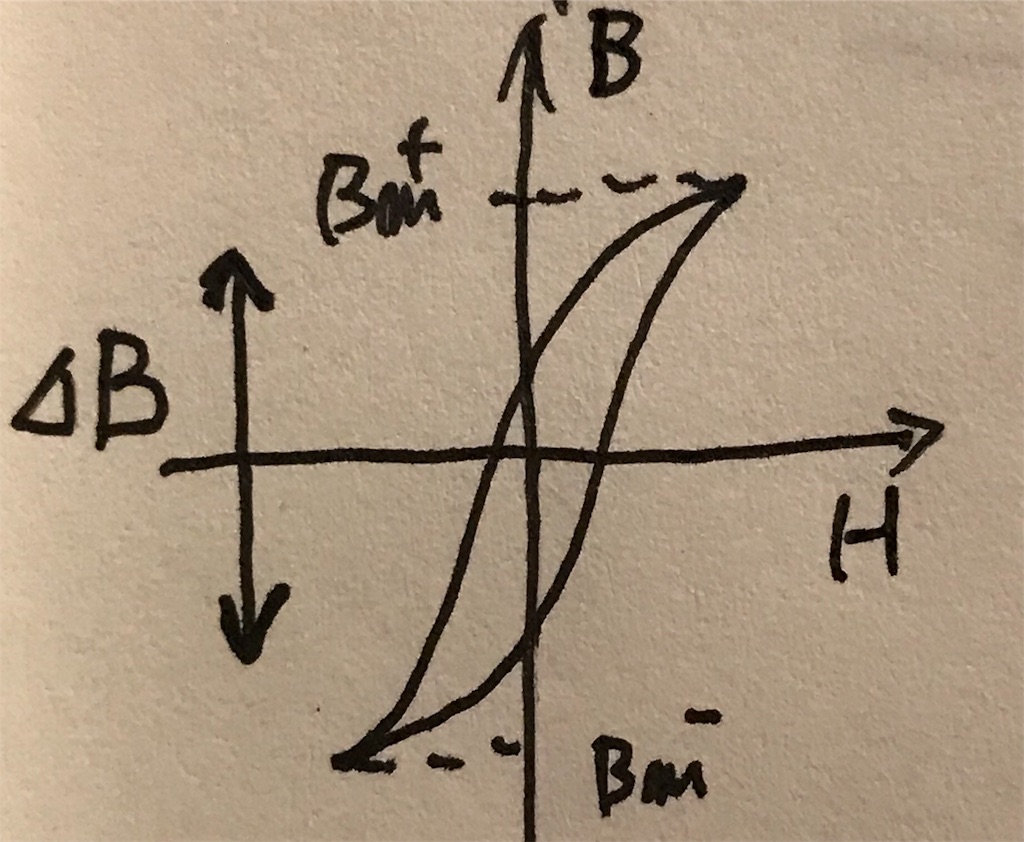
*ΔBについて
ΔBは正側の最大線形部分の磁束密度(Bm+)と負側の最大磁束密度(Bm-)の差となります(下図)(Bm+)=( |Bm-| )より(ΔB = 2・Bm+)となります。
ですが最大磁束密度に近づくほどB-H曲線の傾きである透磁率μが小さくなり、電流が流れすぎたり特性の悪化につながるため、先ほどの値に0.75を掛け、B-H曲線の直線部分を使うようにしましょう。 (ΔB=2・Bm+・0.75)
パルス電圧が正負に振れるため飽和磁束密度がこちらの領域内になります。コアによってまちまちですが、今回は(Bm+ ・ 0.75 = 300mT)としておきましょう。そうすると(ΔB=2*300=600mT)となります。
それでは試しにこの式をつかって計算しましょう。
まずは1次コイルの計算です。
- E=12[V]
- T=10[μS] (共振周波数が60kHzだったので10kHzの余裕を見て50kHzで計算)
- ΔB=600[mT]
- Ae=40[㎟]
これで電卓を打つと
N=5
となります。ですから1次コイルの巻き数は5回です。
次に2次コイルの計算です。ゲートに±15Vをかけたいので
- E=30[V]
- T=10[μS] (50kHz)
- ΔB=600[mT]
- Ae=40[㎟]
とします。
これで電卓を打つと
N=12.5
となります。現実的じゃないので13回ほど巻いておきましょう。
もちろんですが電圧比は巻き数比に比例します。
倍の電圧を得たければ倍の巻き数にすればいいと思います。
2次の巻き数を1次の倍にしたとき、エネルギーが保存されるため、2次コイルに3A流したとすると、1次コイルには約6Aかかるため強力なゲートドライバを作る必要があります。回路図のゲートドライバのFETを高耐流(10A等)のものに変更するといい感じですね!
(GDTに関してはもう少し詳しく別の記事で紹介します。)
GDTの詳しい記事
https://selelab.hatenablog.com/entry/2018/09/24/203909
電源部
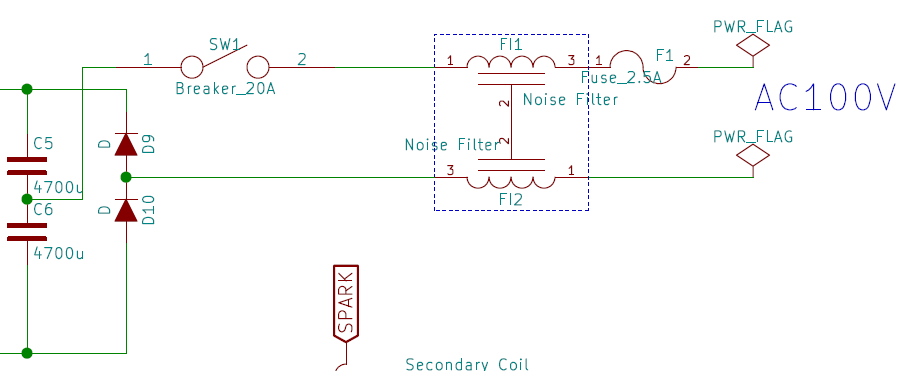
電源部は、商用電源AC100Vを用い、ヒューズ、ノイズフィルター、ブレーカーを介した後、コンデンサ、ダイオードによって倍電圧整流されます。
ヒューズやノイフィルは万が一に備えて使っています。
(ありえんノイズがテスラコイル側の電源で発生した時にコンセントに回り込まないように。)
ブレーカーはスイッチとして使ってます。火花が散りません(雑)
倍電圧整流によって、直流242Vを得ています。
*その後、ブレーカーはSSR(無接点リレー)に置き換わり、ポリスイッチ(4A)を2パラを挟んで運用しました。
おわりに
今回も長ったらしくなってますが、私もまだまだ分からないことばかりでして(特にフィードバック信号と位相とかそのあたりです。)間違ったことを書いていることがあります。
このように記事を書くことで勉強してますのでどうぞ暖かく見守って...等とは言わず、
間違っていましたら是非ご指摘をしていただきたい所存です。
P.S (使い方あってる?)現在、テスラコイルの基板をPCBにして発注をかけています!
届いたら製作して報告しようかと思います。
2018-9

届きました。白レジストはいいですね
学祭ではこちらの基板に頑張ってもらいました。
よく頑張ったね!
オペアンプを作ってみた
はじめに
はじめまして、ハード班の駒形橋です。7月よりSELにて活動をさせていただいています。もっと自己紹介をしたいところですが、顔も見たことない奴のプロフィールなんて誰得な感じなので早速本題に移ります笑
さて、今回はオペアンプをディスクリート(抵抗,トランジスタなどの単体素子)で設計してみました。とはいえド素人丸出しなので、テキトー&ガバガバ設計が随所に見られます...悪しからず...[pic1]

オペアンプとは
オペアンプとは、「OPErational AMPlifier」を略したもので、日本語では「演算増幅器」と呼ばれます。構造は非反転入力と反転入力の二つの入力と一つの出力を備えたIC(集積回路)です。基本動作としては二つの入力に印加した電位の差を増幅します。それ故にオーディオアンプの増幅回路に使われ、他には加算回路や積分回路などの演算回路にも使われます。こうなると「演算増幅器」という名称にも納得ですね!
つくってみた
実は今回は次回以降の製作物の試作という扱いです。ステレオアンプを想定した二回路入りではなく一回路のみ製作します。回路の構成としては、各入力の電圧増幅をトランジスタ(BJT)のエミッタ接地増幅回路で行い、電流増幅をプッシュプルエミッタフォロワ回路で行います。動作の安定のためにトランジスタとダイオードで定電流源を、ダイオードで定電圧源を配置しています。いずれもダイオードの順方向降下電圧を応用しています。(つづきはWEB(Google)で...)回路定数は画像のように決定しました。[pic2]

以下にLTspiceでの回路図(代替部品を使用)とシミュレーション結果を示します。ちゃんと増幅されていて、周波数特性も問題はありません。歪み率も0.002512%と低くていいですね^^(適当)[pic3]

[pic4]

[pic5]

[pic6]

次はユニバーサル基板に実装です。トランジスタはNPN→2SC1815,PNP→2SA1015を、ダイオードは1SS178×3連を、抵抗はカーボン抵抗と金属皮膜抵抗をミックスしたオリジナル合成抵抗を、GNDに落とすコンデンサはセラミックコンデンサの代わりに高級なフィルムコンデンサ!を使いました!(動けばいいんです) こうして完成した基板がこちらです。裏面のパターンも自分にしてはキレイにできました。オシロスコープで波形を確認してみましたが、ちゃんと動作しています!なんとか完成にこぎつけることができました。
[pic7]

[pic8]

[pic9]

[pic10]

[pic11]

[pic12]

まとめ
以上のようにオペアンプをディスクリートで設計動作することができ、トランジスタの基本動作について理解を深めることができました。回路シミュレーションやはんだ付けの作業関連の腕前も少し向上した感じがします。記事をよく見ると若干ネタバレしてますが、次回はこれを用いて何かを作ります!乞うご期待を...
ご覧いただきありがとうございました。ではさようなら!